Absolute Zero: Reinforced Self-play Reasoning with Zero Data
NeurIPS · 2025 · arXiv: arxiv.org/abs/2505.03335
Abstract
Reinforcement learning with verifiable rewards (RLVR) has shown promise in enhancing the reasoning capabilities of large language models by learning directly from outcome-based rewards. Recent RLVR works that operate under the zero setting avoid supervision in labeling the reasoning process, but still depend on manually curated collections of questions and answers for training. The scarcity of high-quality, human-produced examples raises concerns about the long-term scalability of relying on human supervision, a challenge already evident in the domain of language model pretraining. Furthermore, in a hypothetical future where AI surpasses human intelligence, tasks provided by humans may offer limited learning potential for a superintelligent system. To address these concerns, we propose a new RLVR paradigm called Absolute Zero, in which a single model learns to propose tasks that maximize its own learning progress and improves reasoning by solving them, without relying on any external data. Under this paradigm, we introduce the Absolute Zero Reasoner (AZR), a system that self-evolves its training curriculum and reasoning ability by using a code executor to both validate proposed code reasoning tasks and verify answers, serving as an unified source of verifiable reward to guide open-ended yet grounded learning. Despite being trained entirely without external data, AZR achieves overall SOTA performance on coding and mathematical reasoning tasks, outperforming existing zero-setting models that rely on tens of thousands of in-domain human-curated examples. Furthermore, we demonstrate that AZR can be effectively applied across different model scales and is compatible with various model classes.
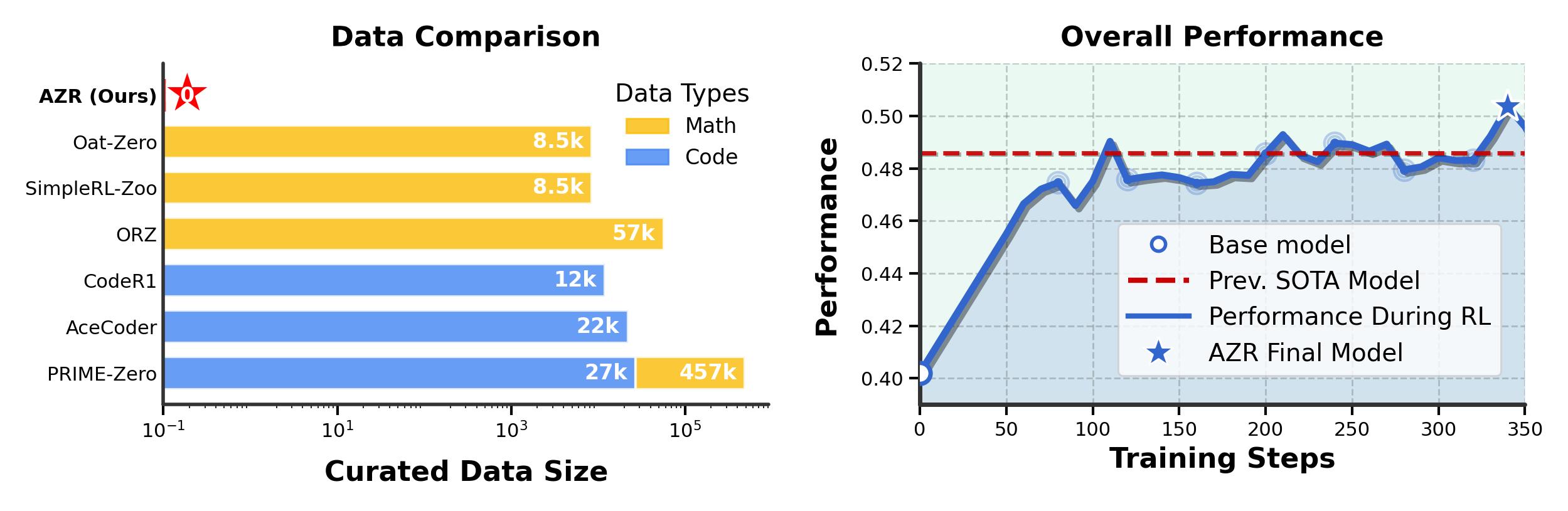
Out-of-Distribution General Reasoning Performance
Absolute Zero Paradigm
Traditional approaches to training reasoning models rely heavily on human-curated data:
- Supervised Fine-Tuning (SFT) requires datasets with human-written queries, rationales, and answers.
- Reinforcement Learning with Verifiable Rewards (RLVR) still needs human-labeled tasks and answers, even if the model generates its own reasoning.
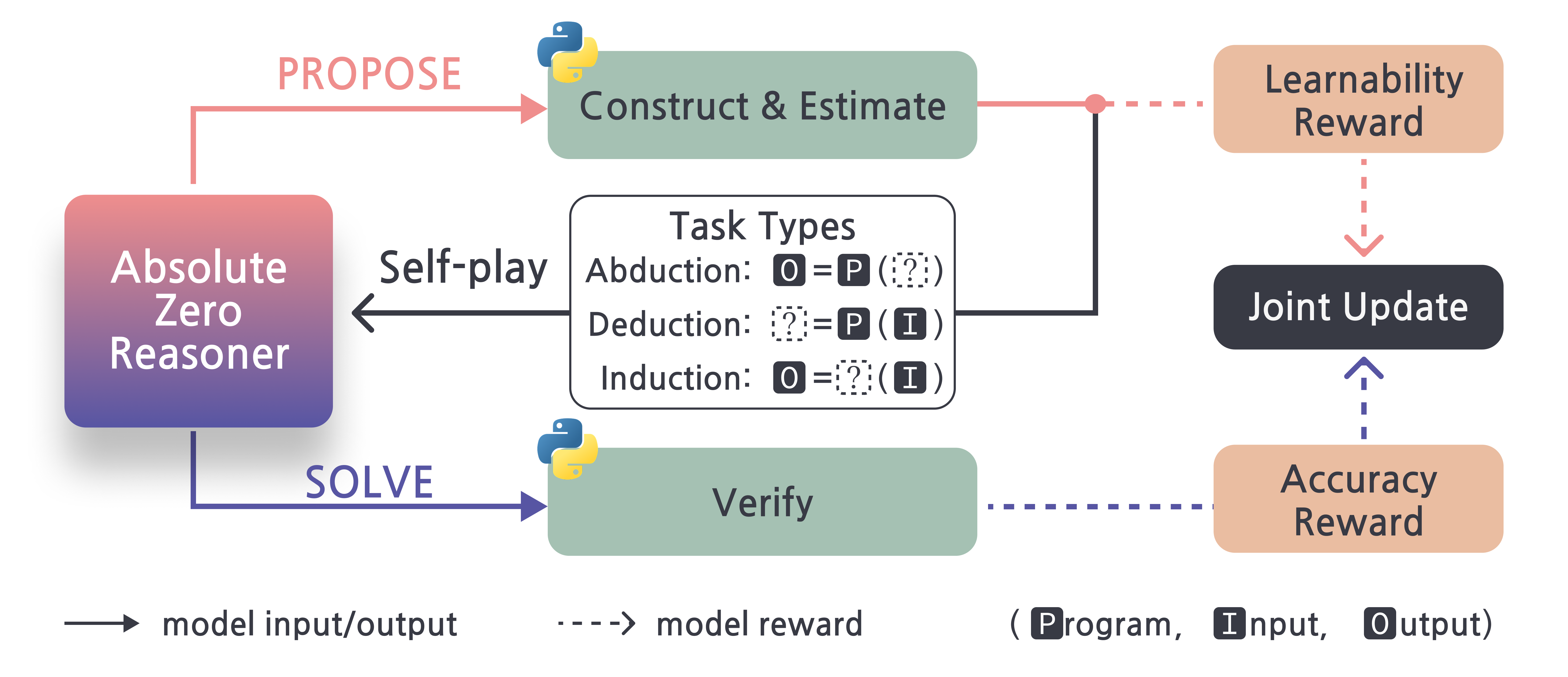
The Absolute Zero paradigm eliminates this dependency on human data. The model simultaneously proposes tasks, solves them, and learns from both stages through self-play. As shown in Figure 1, the agent autonomously creates tasks optimized for learnability and learns to solve them using a unified model.
The agent \(\pi\) acts in two roles: as a proposer \(\pi^{\text{propose}}\) that generates tasks \(\tau\), and as a solver \(\pi^{\text{solve}}\) that produces answers \(y\). The environment e validates proposed tasks into \((x, y\star)\) pairs and provides both learnability rewards \(r^{\text{propose}}\) and solution rewards \(r^{\text{solve}}\). This enables continuous self-improvement without any human-curated data.

Absolute Zero Reasoner
The Absolute Zero Reasoner (AZR) is our first implementation of the Absolute Zero Paradigm. AZR uses a unified language model that serves dual roles while learning through code-based reasoning challenges. The model works through a continuous self-improvement loop without requiring any human-curated data.
Propose and Solve Roles
The Absolute Zero Reasoner employs a unified model that acts in two complementary roles:
- Proposer Role: Generates tasks with high learning potential - neither too easy nor impossible for the current solver. The model is rewarded for creating challenges that provide meaningful learning opportunities.
- Solver Role: Attempts to solve the proposed problems, receiving binary rewards based on the correctness of solutions, verified through Python execution.
For the proposer, we design a specialized reward function based on Monte Carlo rollouts that encourages the generation of tasks with optimal difficulty - problems where the solver sometimes succeeds and sometimes fails. This creates the richest learning signal for continuous improvement.
Reasoning Modes
As shown in Figure 2, the Absolute Zero Reasoner operates across three fundamental reasoning modes, each focusing on different aspects of a triplet (program, input, output):
- Deduction: Predicting the output given a program and input, capturing step-by-step logical reasoning. This tests the model’s ability to trace program execution.
- Abduction: Inferring a plausible input given a program and its output, resembling trial-and-error or search processes. This tests the model’s ability to work backward from results.
- Induction: Synthesizing a program from input-output examples, requiring generalization from partial information. This tests the model’s ability to discover underlying patterns.
Absolute Zero Reasoner Algorithm

Results
Main Results
| Model | Base | #data | HEval+ | MBPP+ | LCBv5 | AME24 | AME25 | AMC | M500 | Minva | Olypiad | CAvg | MAvg | AVG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base Models | ||||||||||||||
| Qwen2.5-7B | - | - | 73.2 | 65.3 | 17.5 | 6.7 | 3.3 | 37.5 | 64.8 | 25.0 | 27.7 | 52.0 | 27.5 | 39.8 |
| Qwen2.5-7B-Ins | - | - | 75.0 | 68.5 | 25.5 | 13.3 | 6.7 | 52.5 | 76.4 | 35.7 | 37.6 | 56.3 | 37.0 | 46.7 |
| Qwen2.5-7B-Coder | - | - | 80.5 | 69.3 | 19.9 | 6.7 | 3.3 | 40.0 | 54.0 | 17.3 | 21.9 | 56.6 | 23.9 | 40.2 |
| Qwen2.5-7B-Math | - | - | 61.0 | 57.9 | 16.2 | 10.0 | 16.7 | 42.5 | 64.2 | 15.4 | 28.0 | 45.0 | 29.5 | 37.3 |
| Zero-Style Reasoners Trained on Curated Coding Data | ||||||||||||||
| AceCoder-RM | Ins | 22k | 79.9 | 71.4 | 23.6 | 20.0 | 6.7 | 50.0 | 76.4 | 34.6 | 36.7 | 58.3 | 37.4 | 47.9 |
| AceCoder-Rule | Ins | 22k | 77.4 | 69.0 | 19.9 | 13.3 | 6.7 | 50.0 | 76.0 | 37.5 | 37.8 | 55.4 | 36.9 | 46.2 |
| AceCoder-RM | Coder | 22k | 78.0 | 66.4 | 27.5 | 13.3 | 3.3 | 27.5 | 62.6 | 29.4 | 29.0 | 57.3 | 27.5 | 42.4 |
| AceCoder-Rule | Coder | 22k | 80.5 | 70.4 | 29.0 | 6.7 | 6.7 | 40.0 | 62.8 | 27.6 | 27.4 | 60.0 | 28.5 | 44.3 |
| CodeR1-LC2k | Ins | 2k | 81.7 | 71.7 | 28.1 | 13.3 | 10.0 | 45.0 | 75.0 | 33.5 | 36.7 | 60.5 | 35.6 | 48.0 |
| CodeR1-12k | Ins | 12k | 81.1 | 73.5 | 29.3 | 13.3 | 3.3 | 37.5 | 74.0 | 35.7 | 36.9 | 61.3 | 33.5 | 47.4 |
| Zero-Style Reasoners Trained on Curated Math Data | ||||||||||||||
| PRIME-Zero | Coder | 484k | 49.4 | 51.1 | 11.0 | 23.3 | 23.3 | 67.5 | 81.2 | 37.9 | 41.8 | 37.2 | 45.8 | 41.5 |
| SimpleRL-Zoo | Base | 8.5k | 73.2 | 63.2 | 25.6 | 16.7 | 3.3 | 57.5 | 77.0 | 35.7 | 41.0 | 54.0 | 38.5 | 46.3 |
| Oat-Zero | Math | 8.5k | 62.2 | 59.0 | 15.2 | 30.0 | 16.7 | 62.5 | 80.0 | 34.9 | 41.6 | 45.5 | 44.3 | 44.9 |
| ORZ | Base | 57k | 80.5 | 64.3 | 22.0 | 13.3 | 16.7 | 60.0 | 81.8 | 32.7 | 45.0 | 55.6 | 41.6 | 48.6 |
| Absolute Zero Training w/ No Curated Data (Ours) | ||||||||||||||
| AZR (Ours) | Base | 0 | 71.3 -1.9 | 69.1 +3.8 | 25.3 +7.8 | 13.3 +6.6 | 13.3 +10.0 | 52.5 +15.0 | 74.4 +9.6 | 38.2 +13.2 | 38.5 +10.8 | 55.2 +3.2 | 38.4 +10.9 | 46.8 +7.0 |
| AZR (Ours) | Coder | 0 | 83.5 +3.0 | 69.6 +0.3 | 31.7 +11.8 | 20.0 +13.3 | 10.0 +6.7 | 57.5 +17.5 | 72.6 +22.6 | 36.4 +19.1 | 38.2 +16.3 | 61.6 +5.0 | 39.1 +15.2 | 50.4 +10.2 |
Scaling Results
| Model Family | Variant | Code Avg | Math Avg | Total Avg |
|---|---|---|---|---|
| Qwen2.5-3B Coder | 51.2 | 18.8 | 35.0 | |
| Qwen2.5-3B Coder | + AZR (Ours) | 54.9 +3.7 | 26.5 +7.7 | 40.7 +5.7 |
| Qwen2.5-7B Coder | 56.6 | 23.9 | 40.2 | |
| Qwen2.5-7B Coder | + AZR (Ours) | 61.6 +5.0 | 39.1 +15.2 | 50.4 +10.2 |
| Qwen2.5-14B Coder | 60.0 | 20.2 | 40.1 | |
| Qwen2.5-14B Coder | + AZR (Ours) | 63.6 +3.6 | 43.0 +22.8 | 53.3 +13.2 |
Given the strong performance of coder models in the 7B category, we extend the analysis by evaluating smaller and larger variants: Qwen2.5-3B-Coder and Qwen2.5-14B-Coder. Due to the absence of existing baselines for these zero-style reasoner models, we compare each model’s performance to its corresponding base coder model.
The results reveal a clear trend: our method delivers greater gains on larger, more capable models. In the in-distribution setting, the 7B and 14B models continue to improve beyond 200 training steps, whereas the smaller 3B model appears to plateau. For out-of-distribution domains, larger models also show greater overall performance improvements than smaller ones: +5.7, +10.2, +13.2 overall performance gains, respectively for 3B, 7B and 14B. This is an encouraging sign, suggesting that scaling enhances the effectiveness of AZR. In future work, we aim to investigate the scaling laws that govern performance in the Absolute Zero paradigm.
Other Key Findings
-
Code priors amplify reasoning. The base Qwen-Coder-7b model started with math performance 3.6 points lower than Qwen-7b. But after AZR training for both models, the coder variant surpassed the base by 0.7 points, suggesting that strong coding capabilities may potentially amplify overall reasoning improvements after AZR training.
-
Cross domain transfer is more pronounced for AZR. After RLVR, expert code models raise math accuracy by only 0.65 points on average, whereas AZR-Base-7B and AZR-Coder-7B trained on self-proposed code reasoning tasks improve math average by 10.9 and 15.2, respectively, demonstrating much stronger generalized reasoning capability gains.
-
Comments as intermediate plans emerge naturally. When solving code induction tasks, AZR often interleaves step-by-step plans as comments and code (see Figure 4), resembling the ReAct prompting framework. Similar behavior has been observed in much larger formal-math models such as DeepSeek Prover v2 (671B). We therefore believe that allowing the model to use intermediate scratch-pads when generating long-form answers may be beneficial in other domains as well.
-
Cognitive Behaviors and Token length depends on reasoning mode. Distinct cognitive behaviors—such as step-by-step reasoning, enumeration, and trial-and-error all emerged through AZR training, but different behaviors are particularly evident across different types of tasks, a canonical example is trial-and-error in abduction, as shown in Figure 5. Furthermore token counts grow over AZR training, but the magnitude of increase also differs by task types: abduction grows the most because the model performs trial-and-error until output matches, whereas deduction and induction grow modestly.
-
Safety alarms ringing. We observe AZR with Llama3.1-8b as the base occasionally produces concerning chains of thought, we term the “uh-oh moment”, example shown in Figure 6, highlighting the need for future work on safety-aware training.



Citation
@inproceedings{zhao2025absolutezero,
title={Absolute Zero: Reinforced Self-play Reasoning with Zero Data},
author={Andrew Zhao and Yiran Wu and Yang Yue and Tong Wu and Quentin Xu and Yang Yue and Matthieu Lin and Shenzhi Wang and Qingyun Wu and Zilong Zheng and Gao Huang},
year={2025},
booktitle = {Advances in Neural Information Processing Systems (NeurIPS)},
url={https://arxiv.org/abs/2505.03335},
}