Patchwise Generative ConvNet: Training Energy-Based Models from a Single Natural Image for Internal Learning
2 Cognitive Computing Lab, Baidu Research, USA

Abstract
Exploiting internal statistics of a single natural image has long been recognized as a significant research paradigm where the goal is to learn the internal distribution of patches within the image without relying on external training data. Different from prior works that model such a distribution implicitly with a top-down latent variable model (e.g., generator), this paper proposes to explicitly represent the statistical distribution within a single natural image by using an energy-based generative framework, where a pyramid of energy functions, each parameterized by a bottom-up deep neural network, are used to capture the distributions of patches at different resolutions. Meanwhile, a coarse-to-fine sequential training and sampling strategy is presented to train the model efficiently. Besides learning to generate random samples from white noise, the model can learn in parallel with a self-supervised task (e.g., recover the input image from its corrupted version), which can further improve the descriptive power of the learned model. The proposed model is simple and natural in that it does not require an auxiliary model (e.g., discriminator) to assist the training. Besides, it also unifies internal statistics learning and image generation in a single framework. Experimental results presented on various image generation and manipulation tasks, including super-resolution, image editing, harmonization, style transfer, etc., have demonstrated the effectiveness of our model for internal learning.
Methodology
Multi-Scale Modeling
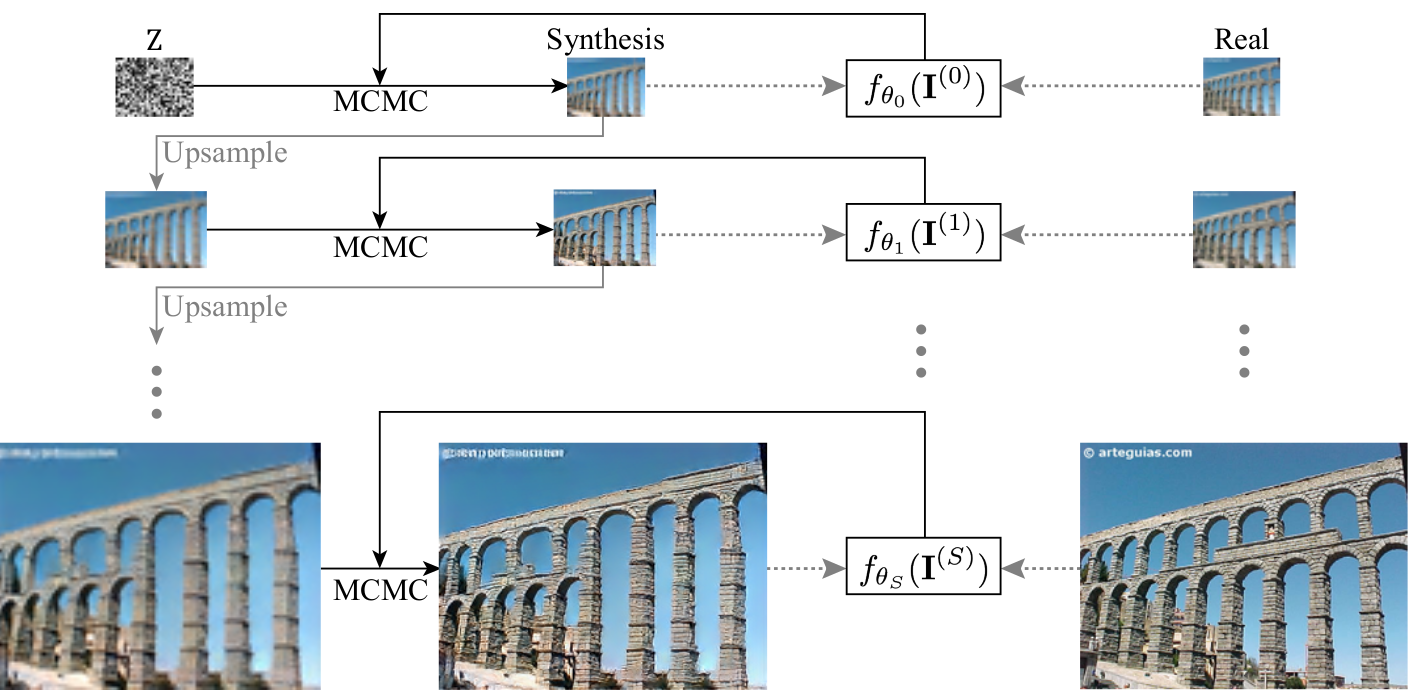 Figure 1. Multi-Scale EBM modeling.
Figure 1. Multi-Scale EBM modeling.
Let \(\{\mathbf{I}(s), s = 0, ..., S\}\) denote the multi-scale versions of a training image \(\mathbf{I}\), with \(s\) indexing the scale, the multi-scale EBM (Figure 1) is modeled as
\[p_\theta(\mathbf{I}^{(s)}) = \frac{1}{Z(\theta_s)} \exp(f_\theta(\mathbf{I}^{(s)})),\]where \(f_\theta\) is an energy network, \(Z(\theta)=\int \exp (f_\theta(\mathbf{I})) d \mathbf{I}\) is a normalization constant.
Multi-Scale Sequential Sampling
 Figure 2. Multi-Scale sequential sampling process.
Figure 2. Multi-Scale sequential sampling process.
The mutli-scale sequential sampling (Figure 2) can be represented as: for \(s=0,...,S\),
\[\tilde{\mathbf{I}}^{(s)}_0= \begin{cases} Z \sim \mathcal{U}_{d}((-1, 1)^{d}) & s=0\\ \text{Upsample}(\tilde{\mathbf{I}}^{(s-1)}_{K^{(s-1)}})& s > 0 \end{cases}\] \[\tilde{\mathbf{I}}^{(s)}_{t+1}= \tilde{\mathbf{I}}^{(s)}_{t} + \frac{\delta^2}{2} \frac{\partial}{\partial \mathbf{I}^{(s)}} f_{\theta_{s}} (\tilde{\mathbf{I}}^{(s)}_{t}) + \delta\epsilon^{(s)}_{t},\]where \(t=0,...,K^{(s)} - 1\) indexes the timestep, \(\mathcal{U}_{d}((-1, 1)^{d})\) the uniform distribution, \(\delta\) the Langvein step size, \(\epsilon_t \sim \mathcal{N}(0, I)\) a Gaussian noise.
Related Work
- Jianwen Xie*, Zilong Zheng*, Xiaolin Fang, Song-Chun Zhu, Ying Nian Wu. “Cooperative Training of Fast Thinking Initializer and Slow Thinking Solver for Conditional Learning.” TPAMI, 2021.
- Jianwen Xie*, Zilong Zheng*, Ruiqi Gao, Wenguan Wang, Song-Chun Zhu, Ying Nian Wu. “Generative VoxelNet: Learning Energy-Based Models for 3D Shape Synthesis and Analysis.” TPAMI, 2020.
- Ruiqi Gao*, Ying Lu*, Junpei Zhou, Song-Chun Zhu, Ying Nian Wu. “Learning Generative ConvNets via Multi-grid Modeling and Sampling.” In CVPR, 2018.
- Jianwen Xie, Yang Lu, Ruiqi Gao, Song-Chun Zhu, Ying Nian Wu. “Cooperative Training of Descriptor and Generator Networks.” TPAMI, 2018.
Acknowledgement
We thank Yang Zhao for helpful discussions, and Yifan Zhang for creating initial image manipulation inputs.
